조합과 순열 4개중 2개 뽑기 예제코드

 

 

#include <iostream>
#include <vector>
#include <algorithm> // next_permutation 사용
using namespace std;

int main() 
{
    vector<int> v = { 1, 2, 3, 4 };  // 예제 데이터
    int cnt = 0;

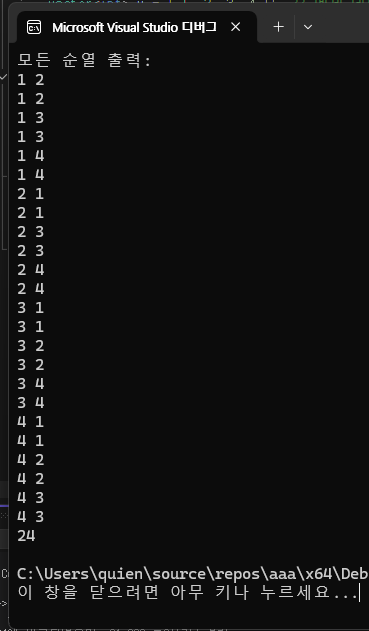
    cout << "모든 순열 출력:" << endl;
    do {
        for (int i = 0; i < 2; i++) cout << v[i] << " ";
        cout << endl;
        cnt++;
        //cout << cnt;
    } while (next_permutation(v.begin(), v.end()));  // 다음 순열 생성

    cout << cnt << endl;
    return 0;
}

 

 

 

 

#include <iostream>
#include <vector>
#include <algorithm> // next_permutation 사용
using namespace std;

int main() {
    int n = 4, r = 2; // 4개 중에서 2개 선택
    vector<int> combination(n, 0);
    fill(combination.end() - r, combination.end(), 1); // 마지막 r개만 1로 설정

    vector<int> elements = { 1, 2, 3, 4 }; // 조합을 만들 원소들

    cout << "모든 조합 출력:" << endl;
    do {
        for (int i = 0; i < n; i++) 
        {
            if (combination[i]) cout << elements[i] << " ";
        }
        cout << endl;
    } while (next_permutation(combination.begin(), combination.end()));

    return 0;
}

• 첫 번째 코드: 순열 (Permutation) → 순서가 중요
• 두 번째 코드: 조합 (Combination) → 순서가 중요하지 않음

---

✅ 1️⃣ 첫 번째 코드 (순열) 실행 결과 검증

#include <iostream>
#include <vector>
#include <algorithm> // next_permutation 사용
using namespace std;

int main() 
{
    vector<int> v = { 1, 2, 3, 4 };  // 예제 데이터
    int cnt = 0;

    cout << "모든 순열 출력:" << endl;
    do {
        for (int i = 0; i < 2; i++) cout << v[i] << " "; // 앞의 2개만 출력
        cout << endl;
        cnt++;
    } while (next_permutation(v.begin(), v.end()));  // 다음 순열 생성

    cout << "총 개수: " << cnt << endl;
    return 0;
}

---

🟢 [순열 결과]

경우의 수 출력 값

1️⃣	1 2
2️⃣	1 3
3️⃣	1 4
4️⃣	2 1
5️⃣	2 3
6️⃣	2 4
7️⃣	3 1
8️⃣	3 2
9️⃣	3 4
🔟	4 1
11️⃣	4 2
12️⃣	4 3

➡ 총 개수 = 4P2 = 4! / (4-2)! = 4 × 3 = 12 (✅ 정답!)

✔ 결과적으로, "4개 중 2개를 순서 있게 뽑는 경우"가 맞다.
✔ next_permutation()을 사용하여 2개씩 출력했기 때문에 올바른 순열을 생성한다.
✔ 순서가 다르면 다른 경우로 처리되므로 순열이 맞다.

---

✅ 2️⃣ 두 번째 코드 (조합) 실행 결과 검증

#include <iostream>
#include <vector>
#include <algorithm> // next_permutation 사용
using namespace std;

int main() {
    int n = 4, r = 2; // 4개 중에서 2개 선택
    vector<int> combination(n, 0);
    fill(combination.end() - r, combination.end(), 1); // 마지막 r개만 1로 설정

    vector<int> elements = { 1, 2, 3, 4 }; // 조합을 만들 원소들

    cout << "모든 조합 출력:" << endl;
    do {
        for (int i = 0; i < n; i++) 
        {
            if (combination[i]) cout << elements[i] << " ";
        }
        cout << endl;
    } while (next_permutation(combination.begin(), combination.end()));

    return 0;
}

---

🔵 [조합 결과]

경우의 수 출력 값

1️⃣	1 2
2️⃣	1 3
3️⃣	1 4
4️⃣	2 3
5️⃣	2 4
6️⃣	3 4

➡ 총 개수 = 4C2 = 4! / (2!(4-2)!) = 6 (✅ 정답!)

✔ "4개 중 2개를 순서 상관없이 뽑는 경우"가 맞다.
✔ (1,2)와 (2,1)이 같은 것으로 처리되므로 조합이 맞다.
✔ next_permutation()을 사용하여 1과 0의 조합을 변환하며 모든 경우를 탐색한다.

---

🔍 결론 (🚀 두 코드 모두 올바르게 동작함!)

코드 개수 특징 결과 검증

순열 (Permutation)	12	순서 O	✅ 4P2 = 12 정확함
조합 (Combination)	6	순서 X	✅ 4C2 = 6 정확함