자료구조&알고리즘/C++

DFS depth first search & BFS breath first search // Tree트리 01

geminanolja 2024. 12. 16. 20:35

그래프 기본 단위 : 정점과 간선으로 이루어진 집합 Gragh

1. 정점(vertex)은 분할 할수 없는 객체(점으로 표현되는 위치, 사람, 또는 물건등이 될수 있음 , 약자로 V or U

2. 간선(Edge) 은 정점을 잇는 선 (관계 또는 경로)

 

Indegree and outdegree

정점에서 나가는 간선 : Outdegree 

정점으로 들어오는 간선 : Indegree

 

가중치 

정점과 정점사이에 드는 비용

(e.g. 우리집(V)에서 판교(U)까지 가는데 드는 택시비용-> V에서 U까지 가는 가중치(=택시비용))

 

 

트리(Tree)는 계층적 구조를 가지며, 사이클이 없는 무방향 그래프

 트리는 여러 가지 중요한 특성을 가지는데, 특히 노드 수와 간선 수 사이의 관계가 중요한 핵심

트리의 정의

  1. 계층적 구조: 부모 노드와 자식 노드로 이루어진 구조
  2. 사이클 없음
  3. 연결된 그래프: 모든 노드는 반드시 하나의 경로를 통해 서로 연결
  4. 무방향 그래프: 트리는 방향성이 없는 간선으로 이루어진 그래프

트리

노드 수(V)와 간선 수(E)의 관계

트리에서 노드의 수를 V (정점 또는 노드 수), 간선의 수를 E라고 할 때, 항상 다음 관계가 성립합니다:

E=V−1E = V - 1

왜 E=V−1E = V - 1 인가?

  1. 트리는 사이클이 없는 연결 그래프.
    • 모든 노드가 연결되어 있으므로 V개의 노드를 연결하기 위해 반드시 V - 1개의 간선이 필요
  2. 사이클이 없는 특성 때문에 불필요한 간선이 존재할 수 없음.
    • 만약 간선이 V개 이상이면 반드시 사이클이 생성되므로 트리가 될 수 없음

예시로 설명

트리 구조 예시:

          1
         / \
        2   3
       / \
      4   5
         / \
        6   7
  1. 노드 수 (VV): 7개
    • 노드: 1, 2, 3, 4, 5, 6, 7
  2. 간선 수 (EE): 6개
    • 간선: (1-2), (1-3), (2-4), (2-5), (5-6), (5-7)

E=V−1=7−1=6E = V - 1 = 7 - 1 = 6

따라서 이 트리는 간선 수가 V−1V - 1이라는 관계를 만족

트리의 속성 요약

  1. **노드 수(V)**와 **간선 수(E)**의 관계:E=V−1E = V - 1트리가 nn개의 노드를 가지고 있다면, 반드시 n−1n - 1개의 간선이 존재
  2. 연결성: 모든 노드가 하나의 경로를 통해 연결
  3. 사이클 없음

루트 노드 : 가장 위에 있는 노드// 트리 탐색시 루트노드를 중심으로 탐색하면 문제가 쉽게 풀림

내부 노드 : 루트 및 리프노드 사이노드

리프노드 : 자식노드가 없는 노드

 

트리 높이, 레벨

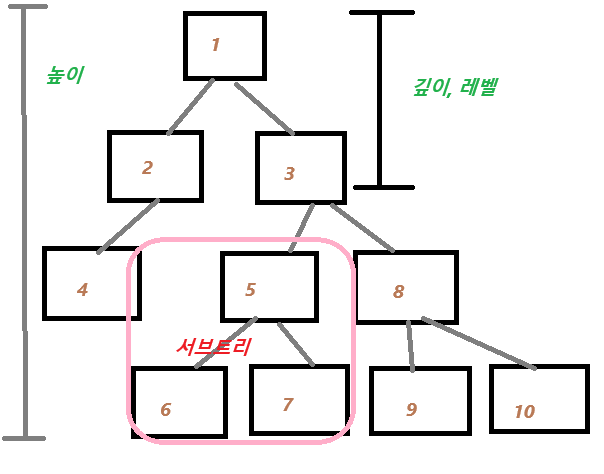
깊이 : 루트에서 해당 노드까지의 최단거리 (e.g. 5번 노드의 깊이는 2)

높이 : 루트노드에서 리프노드까지의 거리중 가장 긴 거리 (e.g. : 위의 트리는 높이가 3)

레벨 : 트리의 레벨은 문제마다 조금씩 다르지만 보통 깊이와 같은 의미

         1번 노드가 0레벨이라면 2번노드는 1레벨// 민약 1번노드를 1레벨이라고 하면 2번노드는 2레벨

서브 트리 : 트리 내의 하위 집합// 트리내에 있는 부분집합